10. Dijkstra algorithm

Dijkstra algorithm: directed, shortest path

743. Network Delay TimeMedium6.4K334Companies

You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.

We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.

Example 1:

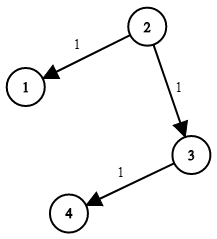
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2

Example 2:

Input: times = [[1,2,1]], n = 2, k = 1
Output: 1

Example 3:

Input: times = [[1,2,1]], n = 2, k = 2
Output: -1

Constraints:

• 1 <= k <= n <= 100

• 1 <= times.length <= 6000

• times[i].length == 3

• 1 <= ui, vi <= n

• ui != vi

• 0 <= wi <= 100

• All the pairs (ui, vi) are unique. (i.e., no multiple edges.)

Network Delay Time - LeetCodeLeetCode

with visited checking

We do not need to visit a vertex already visited cuz visited vertex got a shortest path already from a start vertex

/**
 * @param {number[][]} times
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var networkDelayTime = function (times, n, k) {
    // create adjs

    // adjecent list
    const adjs = {};
    // minimum dist at vertex i
    const dist = [];
    // vertex where relaxation is done
    const visited = new Set();
    // track prev vertex connected to current i
    const ids = [];

    // initialize
    for (let i = 0; i <= n; i++) {
        adjs[i] = [];
        ids[i] = i;
        dist[i] = Infinity;
    }

    // create adjecent list
    for (const [u, v, w] of times) {
        adjs[u].push([v, w]);
    }

    // heap to track current vertex, no visited and minimum 
    const minHeap = new Heap([], (a, b) => a[1] <= b[1]);
    
    // insert start vertex with distance 0
    minHeap.insert([k, 0]);
    dist[k] = 0;

    while (minHeap.size > 0) {
        // console.log('before:: ', minHeap.heap);
        const [here, currentWeight] = minHeap.remove();

        // other than using visited arr, we can just filter visited vertex by doing this
        // property a -> b -> c, a -> c is shortest path then a->b, b -> c also shortest
        // if (dist[here] < currentWeight) continue;
        
        const adj = adjs[here];
        for (const [there, w] of adj) {
            if (visited.has(there)) 
                continue;
            
            // current min distance to vertex there from start
            const prev = dist[there];
            
            // dist[here] is equal to currentWeight if we do not put visited vertex again into the heap
            const next = dist[here] + w; 
            
            if (prev > next) {
                // change prev vertex
                ids[there] = here;
                // update minimum distance 
                dist[there] = next;

                minHeap.insert([there, next]);
            }
        }
        // console.log('after:: ', minHeap.heap);

        visited.add(here); 
    }

    let max = -Infinity;
    // vertex starts from 1
    for (let i = 1; i <= n; i++) {
        if (dist[i] === Infinity) return -1;
        max = Math.max(dist[i], max);
    }

    return max;
};

class Heap {
    constructor(arr, predicate = (a, b) => a <= b) {
        this.predicate = predicate;
        this.size = arr.length;
        this.heap = this.buildHeap(arr);
    }

    buildHeap(arr) {
        let currentIndex = Math.floor((arr.length - 1 - 1) / 2);
        while (currentIndex >= 0) {
            this.siftDown(arr, currentIndex, arr.length - 1);
            currentIndex--;
        }

        return arr;
    }

    insert(v) {
        this.heap.push(v);
        this.size++;

        this.siftUp(this.heap, this.heap.length - 1);

    }

    remove(v) {
        this.swap(this.heap, 0, this.heap.length - 1);
        const elementToRemove = this.heap.pop();
        this.size--;
        
        this.siftDown(this.heap, 0, this.heap.length - 1);
        return elementToRemove;
    }

    siftUp(heap, currentIndex) {
        let parentIndex = Math.floor((currentIndex - 1) / 2);
        while (parentIndex >= 0) {
            if (this.predicate(heap[parentIndex], heap[currentIndex])) {
                break;
            }

            this.swap(heap, parentIndex, currentIndex);
            currentIndex = parentIndex;
            parentIndex = Math.floor((currentIndex - 1) / 2);
        }
        return heap;
    }

    siftDown(heap, currentIndex, endIndex) {
        let left = currentIndex * 2 + 1;

        while (left <= endIndex) {
            let min = left;
            const right = currentIndex * 2 + 2;
            if (heap[right] !== undefined && this.predicate(heap[right], heap[min])) {
                min = right;
            }

            if (this.predicate(heap[currentIndex], heap[min])) break;
            this.swap(heap, currentIndex, min);
            currentIndex = min;
            left = currentIndex * 2 + 1;
        }

        return heap;
    }

    swap(arr, a, b) {
        [arr[b], arr[a]] = [arr[a], arr[b]];
    }

}

without visited checking

LeetCode - The World's Leading Online Programming Learning Platform

/**
 * @param {number[][]} times
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var networkDelayTime = function (times, n, k) {
    // create adjs

    // adjecent list
    const adjs = {};
    // minimum dist at vertex i
    const dist = [];
    // track prev vertex connected to current i
    const ids = [];

    // initialize
    for (let i = 0; i <= n; i++) {
        adjs[i] = [];
        ids[i] = i;
        dist[i] = Infinity;
    }

    // create adjecent list
    for (const [u, v, w] of times) {
        adjs[u].push([v, w]);
    }

    // heap to track current vertex, no visited and minimum 
    const minHeap = new Heap([], (a, b) => a[1] <= b[1]);
    
    // insert start vertex with distance 0
    minHeap.insert([k, 0]);
    dist[k] = 0;

    while (minHeap.size > 0) {
        const [here, currentWeight] = minHeap.remove();

        // other than using visited arr, we can just filter visited vertex by doing this
        // property a -> b -> c, a -> c is shortest path then a->b, b -> c also shortest
        // if (dist[here] < currentWeight) continue;
        
        const adj = adjs[here];
        for (const [there, w] of adj) {
            
            // current min distance to vertex there from start
            const prev = dist[there];
            
            // dist[here] is equal to currentWeight if we do not put visited vertex again into the heap
            const next = dist[here] + w; 
            
            if (prev > next) {
                // change prev vertex
                ids[there] = here;
                // update minimum distance 
                dist[there] = next;

                minHeap.insert([there, next]);
            }
        }
    }

    let max = -Infinity;
    // vertex starts from 1
    for (let i = 1; i <= n; i++) {
        if (dist[i] === Infinity) return -1;
        max = Math.max(dist[i], max);
    }

    return max;
};

class Heap {
    constructor(arr, predicate = (a, b) => a <= b) {
        this.predicate = predicate;
        this.size = arr.length;
        this.heap = this.buildHeap(arr);
    }

    buildHeap(arr) {
        let currentIndex = Math.floor((arr.length - 1 - 1) / 2);
        while (currentIndex >= 0) {
            this.siftDown(arr, currentIndex, arr.length - 1);
            currentIndex--;
        }

        return arr;
    }

    insert(v) {
        this.heap.push(v);
        this.size++;

        this.siftUp(this.heap, this.heap.length - 1);

    }

    remove(v) {
        this.swap(this.heap, 0, this.heap.length - 1);
        const elementToRemove = this.heap.pop();
        this.size--;
        
        this.siftDown(this.heap, 0, this.heap.length - 1);
        return elementToRemove;
    }

    siftUp(heap, currentIndex) {
        let parentIndex = Math.floor((currentIndex - 1) / 2);
        while (parentIndex >= 0) {
            if (this.predicate(heap[parentIndex], heap[currentIndex])) {
                break;
            }

            this.swap(heap, parentIndex, currentIndex);
            currentIndex = parentIndex;
            parentIndex = Math.floor((currentIndex - 1) / 2);
        }
        return heap;
    }

    siftDown(heap, currentIndex, endIndex) {
        let left = currentIndex * 2 + 1;

        while (left <= endIndex) {
            let min = left;
            const right = currentIndex * 2 + 2;
            if (heap[right] !== undefined && this.predicate(heap[right], heap[min])) {
                min = right;
            }

            if (this.predicate(heap[currentIndex], heap[min])) break;
            this.swap(heap, currentIndex, min);
            currentIndex = min;
            left = currentIndex * 2 + 1;
        }

        return heap;
    }

    swap(arr, a, b) {
        [arr[b], arr[a]] = [arr[a], arr[b]];
    }

}

without visited checking and adding filter condition

while (minHeap.size > 0) {
        const [here, currentWeight] = minHeap.remove();

        // other than using visited arr, we can just filter visited vertex by doing this
        // property a -> b -> c, a -> c is shortest path then a->b, b -> c also shortest
        if (dist[here] < currentWeight) continue;
        
        const adj = adjs[here];
        for (const [there, w] of adj) {
            
            // current min distance to vertex there from start
            const prev = dist[there];
            
            // dist[here] is equal to currentWeight if we do not put visited vertex again into the heap
            const next = dist[here] + w; 
            
            if (prev > next) {
                // change prev vertex
                ids[there] = here;
                // update minimum distance 
                dist[there] = next;

                minHeap.insert([there, next]);
            }
        }
    }